Peluang Suatu Kejadian
1. Pengertian Percobaan, Kejadian, dan Ruang Sampel
Percobaan adalah suatu tindakan atau kegiatan yang dapat diulang dengan keadaan yang sama untuk memperoleh hasil tertentu. Kejadian sederhana adalah kejadian beranggotakan tepat satu ruang sampel. Ruang sampel adalah himpunan semua titik sampel atau himpunan semua hasil yang mungkin dari suatu percobaan. Ruang sampel dinotasikan dengan S. Titik sampel adalah setiap anggota dari ruang sampel.
Setiap kali melakukan percobaan akan diperoleh hasil kejadian. Kejadian merupakan himpunan bagian dari ruang sampel. Banyaknya anggota ruang sampel biasanya dilambangkan dengan n(S).
2.Peluang Suatu Kejadian
Jika A adalah suatu kejadian yang terjadi pada suatu percobaan dengan ruang sampel S, di mana setiap titik sampelnya mempunyai kemungkinan sama untuk muncul maka peluang dari suatu kejadian A dirumuskan sebagai berikut.
Dengan :
P (A) = peluang kejadian A
n (A) = banyak anggota A
n (S) = banyak anggota ruang sampel S
3. Kisaran Nilai Peluang
Nilai peluang suatu kejadian adalah 0 ≤ P(A) ≤ 1 dengan A merupakan kejadian pada percobaan tersebut.
Jika P(A) = 0 maka kejadian Atidak mungkin (mustahil) terjadi.
Jika P(A) = 1 maka kejadian A pasti terjadi.
4. Frekuensi Harapan
Frekuensi harapan suatu kejadian adalah frekuensi yang diharapkan terjadinya kejadian tersebut selama n percobaan. Frekuensi harapan dari sejumlah kejadian merupakan banyaknya kejadian dikalikan dengan peluang kejadian itu. Frekuensi harapan dirumuskan sebagai berikut.
Dengan
Fh (A) = frekuensi harapan kejadian A
n = banyak percobaan
P (A) = peluang kejadian A
5. Komplemen suatu kejadian
A adalah kejadian pada sebuah ruang sampel sedangkan Ac adalah kejadian bukan A yang juga terdapat pada ruang sampel tersebut. Hubungan antara kejadian A dan kejadian bukan dirumuskan sebagai berikut.
Dengan
P(A) = peluang kejadian A
P (Ac) = peluang bukan kejadian A
6. Peluang Kejadian Majemuk
- Peluang dua kejadian tidak saling lepas
Misalkan A dan B masing-masing kejadian dalam ruang sampel S. Gabungan kejadian Aatau B (dinotasikan Au B) adalah himpunan semuatitik sampel yang terdapat pada kejadian Aatau B atau keduanya. Jika A dan B adalah dua kejadian yang tidak saling lepas maka berlaku:
Peluang Dua Kejadian Saling Lepas
Kejadian A dan B dikatakan saling lepas jika kejadian A dan B tidak dapat terjadi bersama-sama atau An B = 0atauP(An B) = O.Jika A dan B adalah dua kejadian yang saling lepas maka berlaku:

Dua Kejadian Saling Bebas
Kejadian A dan B dikatakan saling bebas jika kejadian A dan B tidak saling memengaryhi. Artinya, terjadi atau tidak terjadinya kejadian A tidak memengaruhi terjadi atau tidak terjadinya kejadian B. Jika A dan B adalah dua kejadian yang saling bebas maka berlaku:
Dua Kejadian Tidak Saling Bebas (Bersyarat)
Jika kejadian A dan B dapat terjadi bersama-sama, tetapi terjadi atau tidak terjadinya kejadian A akan memengaruhi terjadi atau tidak terjadinya kejadian B maka kejadian seperti ini dinamakan kejadian tidak saling bebas atau kejadian bersyarat . Jika A dan B adalah kejadian bersyarat maka berlaku:

Demikian Penjelasan lengkap yang diberikan tentang materi peluang matematika dan rumus soal, Semoga pembaca dapat memahami materi yang diberikan, dan ilmu yang dibagikan dapat bermanfaat bagi pembaca. Sampai jumpa di artikel lainnya …
Setiap kali melakukan percobaan akan diperoleh hasil kejadian. Kejadian merupakan himpunan bagian dari ruang sampel. Banyaknya anggota ruang sampel biasanya dilambangkan dengan n(S).
P (A) = peluang kejadian A
n (A) = banyak anggota A
n (S) = banyak anggota ruang sampel S
Jika P(A) = 0 maka kejadian Atidak mungkin (mustahil) terjadi.
Jika P(A) = 1 maka kejadian A pasti terjadi.
Dengan
Fh (A) = frekuensi harapan kejadian A
n = banyak percobaan
P (A) = peluang kejadian A
Fh (A) = frekuensi harapan kejadian A
n = banyak percobaan
P (A) = peluang kejadian A
5. Komplemen suatu kejadian
A adalah kejadian pada sebuah ruang sampel sedangkan Ac adalah kejadian bukan A yang juga terdapat pada ruang sampel tersebut. Hubungan antara kejadian A dan kejadian bukan dirumuskan sebagai berikut.
Dengan
P(A) = peluang kejadian A
P (Ac) = peluang bukan kejadian A
P(A) = peluang kejadian A
P (Ac) = peluang bukan kejadian A
6. Peluang Kejadian Majemuk
- Peluang dua kejadian tidak saling lepas
Misalkan A dan B masing-masing kejadian dalam ruang sampel S. Gabungan kejadian Aatau B (dinotasikan Au B) adalah himpunan semuatitik sampel yang terdapat pada kejadian Aatau B atau keduanya. Jika A dan B adalah dua kejadian yang tidak saling lepas maka berlaku:
Peluang Dua Kejadian Saling Lepas
Kejadian A dan B dikatakan saling lepas jika kejadian A dan B tidak dapat terjadi bersama-sama atau An B = 0atauP(An B) = O.Jika A dan B adalah dua kejadian yang saling lepas maka berlaku:

Dua Kejadian Saling Bebas
Kejadian A dan B dikatakan saling bebas jika kejadian A dan B tidak saling memengaryhi. Artinya, terjadi atau tidak terjadinya kejadian A tidak memengaruhi terjadi atau tidak terjadinya kejadian B. Jika A dan B adalah dua kejadian yang saling bebas maka berlaku:
Dua Kejadian Tidak Saling Bebas (Bersyarat)
Jika kejadian A dan B dapat terjadi bersama-sama, tetapi terjadi atau tidak terjadinya kejadian A akan memengaruhi terjadi atau tidak terjadinya kejadian B maka kejadian seperti ini dinamakan kejadian tidak saling bebas atau kejadian bersyarat . Jika A dan B adalah kejadian bersyarat maka berlaku:

Demikian Penjelasan lengkap yang diberikan tentang materi peluang matematika dan rumus soal, Semoga pembaca dapat memahami materi yang diberikan, dan ilmu yang dibagikan dapat bermanfaat bagi pembaca. Sampai jumpa di artikel lainnya …

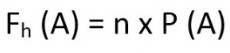
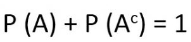

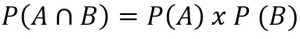
Tidak ada komentar:
Posting Komentar